Minimum and maximum level constraints
This is work in progress! The content is still incomplete and changing.
This is Part 3 of the sign consistency series. Previously, we covered the sign consistency rule for backward propagation. In this part I will introduce a new rule that discards solutions that violate minimum and maximum constraints on system variables.
Constrained values for system variables
A lot of variables in biological systems have minimum (resp. maximum) constraints. Concentration level cannot go below 0 or above 100%, and signals which are below the detection threshold cannot drop any further. Figure 1 shows an IG with four variables a, b, c and d. Let’s say the variable c represent a concentration and only values in the range of 0 to 100 are valid. Further, we know that in our reference state SR the variable c is at its minimum. Let’s try to find all labelings μi that represent transisitions from SR to a state Si where the level of d has increased, μi(d) = +. Figure 2 shows all labelings μi that satisfy consistency Rule 1. The labelings μ2 and μ3 violate the the minimality constraint on variable c, because there exists no value for c in [0,100] such that sign(c - 0) = –.
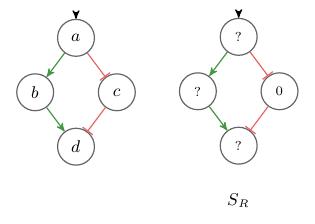
Fig. 1: An IG and with the reference state SR where variable c on its minimum.
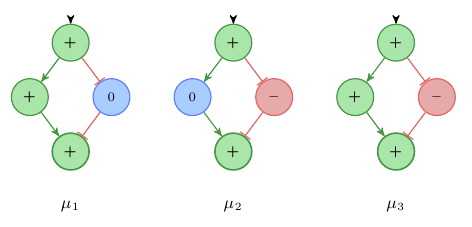
Fig. 2: All labelings μi with μi(d) = + that satisfy Rule 1. Only μ1 is consistent with the value restrictions of variable c.
To deal with minimum (resp. maximum) constraints we introduce a new consistency rule.
Rule 2 (obey minima/maxima): A variable that is on its minimum cannot decrease and an variable at its maximum cannot increase. Let (V,E,σ) be an IG, MIN ⊆ V variables that are at their minimum, and MAX ⊆ V variables that are at their maximum. Then a labeling μ : V →{+,–,0} satisfies Rule 2 for node i ∈ V iff
- μ(i) = 0, or
- μ(i) = –, and i ∉ MIN, or
- μ(i) = +, and i ∉ MAX.
Rule 2 allows us to exclude solutions that violate the constraints on minimal/maximal values. In Figure 2 only labeling μ1 satisfies both consistency rules 1 and 2.
Conclusion
We now have a consistency rule that allows us to filter solutions that violate constraints restricting the minimum or maximum level of system variables. This rule can be combined with other consistency rules to get better explanations for state transitions. In the next part I will introduce another consistency rule that increases the predictive power of sign consistency methods.