Excluding unfounded changes in feedback loops
This is work in progress! The content is still incomplete and changing.
This is Part 6 of the sign consistency series. In this part I will introduce a new global consistency rule to ensure that every change is justified by a chain of influences that can be traced back to an input node. This natural constraint is especially useful to exclude self-justification of changes via positive feedback loops.
Circular regulation
In most biological systems we find self regulation via feedback loops. The consistency rules that we’ve covered so far allow circular explanation. This poses the problem that they allow state transitions for which we can not identify the reason that triggered the state change. For example in Figure 1 we see an IG with labelings that explain an increase in d. Both total labelings satisfy the propagation rules (Rule 1 and 3). For μ1 we see a circular up regulation in b and c, which is used as explanation for the increase in d, but we don’t know why b and c have increase in the first place. Only the labeling μ2 allows us to identify a trigger for the state change, i.e. the increase in a.
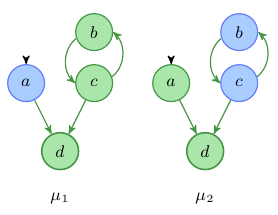
Fig. 1: Example for an influence graph with self regulation. An increase in d can be explained either by self activation in b and c or by the input node a.
To filter labelings which represent circular explanations we introduce the following consistency rule.
Rule 4 (a change must be founded in an input): Let (V,E,σ) be an IG and I ⊆ V the input nodes. Then a labeling μ : V →{+,–,0} satisfies Rule 4 for i ∈ V if
- i ∈ I, or
- μ(i) = 0, or
- there exist a path (v0,…,vk) in E with v0 ∈ I, vk = i and μ(vn-1)σ(vn-1,vn) = μ(vn) for all n = 1…k.
Using Rule 4 we can avoid manual removal of positive feedback loops as done in other approaches, and identify state transitions which can be explained by external perturbations. Only the labeling μ2 satisfies Rule 4. Consistency rule 4 is especially useful if we want apply sign consistency methods in the context of perturbation experiments. When we are actually interested in the response to perturbations, or if we want to identify possible perturbations that trigger desired state transitions.
Conclusion
This part introduced a consistency rule that allows us to exclude unfounded self regulations. In the next part I will show how we can relate our model to actual measurement data via sign constraints.